이중 for문 쓰지 마세요?
항상 개발할때 듣던말이 있다. 이중 for문 쓰지 마라!
왜 쓰지 말라는건지에 대해서 생각하면 다음과 같다.
function hasDuplicateBruteForce(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = i + 1; j < arr.length; j++) { // 모든 쌍을 비교
if (arr[i] === arr[j]) {
return true;
}
}
}
return false;
}function hasDuplicateOptimized(arr) {
const seen = new Set();
for (let num of arr) {
if (seen.has(num)) {
return true;
}
seen.add(num);
}
return false;
}배열을 한번만 돌면 되는걸 몇번을 더 도니까 이게 너무 비효율적이니까 하지말라는거다.
그런데... 어떻게 비효율적인가? 왜 비효율적이라고 생각하고, 어떤기준으로 판단하는건가?
거기서 시간복잡도랑 공간복잡도가 나온다!
이사람 알고리즘 좀 하는데...? 의 기준은 코드의 길이도, 가독성도 아닌 시간복잡도와 공간복잡도이다. 코테에서 공간복잡도로 고생할일은 어지간하면 없으므로 공간복잡도는 제외한다!
시간복잡도가 뭔데?
시간이 얼마나 많이 드냐? 보다는 입력의 값이 커지면 커질수록 어떤 기울기로 연산의 갯수가 많아지는가? 라고 이해하면 편함
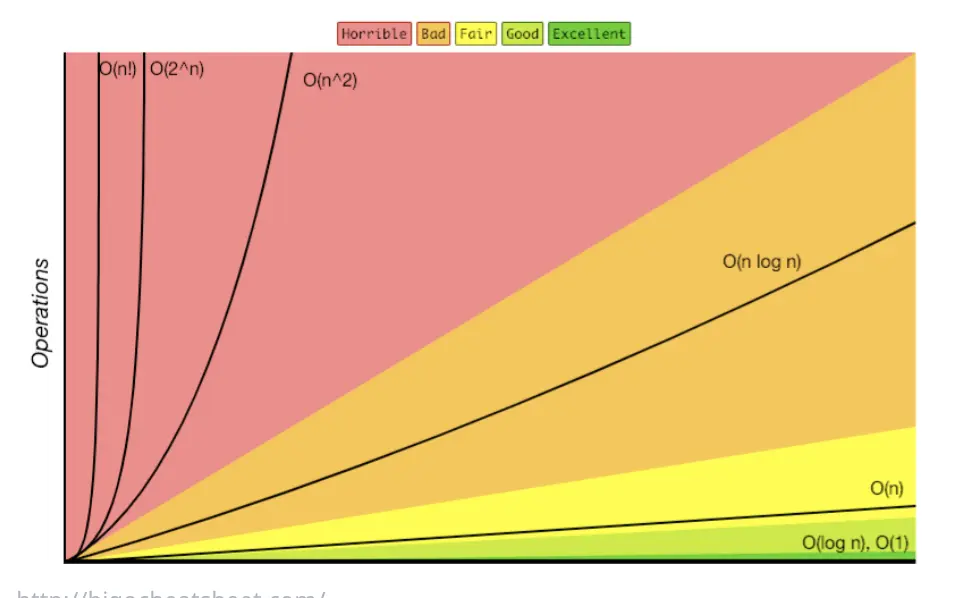
O(N) = 입력이 증가하면 처리시간이 선형적으로 증가함
O(N^2) = 입력이 증가하면 할수록 더 큰 폭으로 처리시간이 증가함.
어렵게 생각하지 말기
input으로 길이가 5인 배열을 받았다고 생각해보자
input을 한번씩 돌면서 sum이라는 변수에 1씩 더하는 함수가 있다고 쳐보자.
let sum = 0;
for(let i = 0 ; i < input.lenth; i++){
sum+=1;
}총 5번 돌기만 하고, 그 안에는 ... 5와 관련된 그 어떤 로직도 없다. 그냥 더하기만 한다.
그러니 input길이가 10이 되어도 그냥 10번 연산하게 될거다.
그러면 이중for문이면?
let sum = 0;
for(let i = 0 ; i < input.lenth; i++){
for(let j = 0; j < input.length; j++){
sum+=1;
}
}input의 값이 5이면 이 로직은 25번 연산한다.
input의 값이 10이면 이 로직은 100번 연산한다.
헉쓰... 너무 갑자기 커지는거 아녀?
아까 애들은 그냥 input 길이가 5늘어나면 연산도 5번 늘어났는데여기는 input 길이가 5늘어나면 연산이 75번이 늘어나ㅜㅜ
=> 이게 핵심! 반복문안에(N번 연산하는 놈) 또 반복문이 있으면(N번 연산하는 넘) O(N*N) = O(N^2)
이라고 부르는 것 뿐임.
다른 계산도 동일하다!
입력한 값에 대해서 내가 멀 입력해도 달라지는게 없음 : O(1)N = 1,000,000 넣어도 연산은 한번이에용
입력한 값이 커져도 연산회수가 조금씩만 증가함 : O(logN)N = 1,000,000 넣으면 연산 20번만해요!
예시코드
O(1)
function getFirstElement(arr) {
return arr[0]; // 항상 한 번만 실행됨
}O(N) => 반복문이 N번만큼 반복되고, 그 안에서 연산이 1번 있음
function sumArray(arr) {
let sum = 0;
for (let i = 0; i < arr.length; i++) { // 배열 크기만큼 반복
sum += arr[i];
}
return sum;
}O(N^2) => 반복문이 N번만큼 반복되고, 그 안에서 반복문이 N번 반복되고, 그 안에선 연산이 하나 있음.
N*N 만큼 연산을 하게 될테니, O(N^2)이라고 한다.
function hasDuplicateBruteForce(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = i + 1; j < arr.length; j++) {
if (arr[i] === arr[j]) return true;
}
}
return false;
}더 많은 시간복잡도?
| 시간 복잡도 | 어디에서 쓰이는지 | 예제 |
|---|---|---|
| O(1) | 특정 값 접근, 단순 연산 | 배열 인덱스 arr[i], 해시맵 map.get(key) |
| O(log N) | 이진 탐색, 균형 트리 탐색 | binary search, set.has(), map.get() (Red-Black Tree 기반) |
| O(N) | 단순 반복문, 배열 탐색 | for 문, 리스트 탐색 |
| O(N log N) | 효율적인 정렬, 분할 정복 알고리즘 | 퀵 정렬, 병합 정렬, 세그먼트 트리 |
| O(N²) | 이중 반복문 (브루트포스) | 버블 정렬, 선택 정렬, 중복 검사 |
| O(2^N) | 부분 집합, 완전 탐색 (백트래킹) | 모든 경우의 수 탐색 (DFS) |
| O(N!) | 순열, 조합 문제 | TSP (외판원 문제), NP-완전 문제 |
전부다 설명하는것보다 필요한걸 본인이 더 공부해보는 방식을 추천한다. 그냥 아, 맵을 쓰면 O(1)이구나... 이진탐색은 O(logN)이구나... 하고 넘어가놓고 코드에 적용해보세용.
어떤 문제에서 어떤 알고리즘 써야하냐?
이런 제한사항을 꽤 봤을텐데, 이는 어떤 알고리즘을 쓰냐에 대한 힌트이다! 엥 내 계산상 저정도는 절대 안나오는데... 싶으면 다른 알고리즘을 써야한다.

입력의 크기에 따라서 사용되는 알고리즘이 달라지기때문에, 우리는 시간복잡도를 계산할 필요가 있는것이다. 입력 크기를 본뒤에 해당 문제를 풀어보고, 어떤 알고리즘이 가능한지 암기하는 생활을 해보도록 하자.
입력 크기 (N) |
추천 알고리즘 | 비고 |
|---|---|---|
| N ≤ 10 | O(N!), O(2^N) 가능 |
완전 탐색 (백트래킹, 순열) |
| N ≤ 20 | O(2^N) 가능 |
비트마스크, 부분집합 탐색 |
| N ≤ 100 | O(N^3) 가능 |
플로이드-워셜, 3중 for문 |
| N ≤ 10,000 | O(N^2) 가능 |
DP (O(N^2)), 단순 그래프 탐색 |
| N ≤ 1,000,000 | O(N log N), O(N) 필요 |
정렬 (O(N log N)), 해시, 세그먼트 트리 |
| N ≥ 10,000,000 | O(log N), O(1) 필요 |
이진 탐색, 해시, 그리디 |
1초안에 보통 10^8 번의 연산을 할수있거든요? 세상이 그렇습니다... 그래서 10,000,000 = 10^7 이니까 만약 여기서 시간복잡도가 O(N)이 됐다간...
function fastLoop(n) {
let sum = 0;
for (let i = 0; i < n; i++) { // O(N)
sum += i; // 단순 덧셈 (O(1))
}
return sum;
}이거는 통과할수있는데
function slowLoop(n) {
let result = "";
for (let i = 0; i < n; i++) { // O(N)
result += "a"; // 문자열 연결은 O(N) → 전체적으로 O(N^2)처럼 동작할 수도 있음!
}
return result;
}
console.log(slowLoop(10_000_000)); // 실행하면 느려짐 (시간 초과 가능)이런건 통과 못함(결과적으로 O(N^2)이라서 통과 못하는거지만!) 10^7 을 마주했으면 안전하게 logN정도의 알고리즘을 찾아보는게 좋다.
근데... 알고리즘이 모죠?
저희가 앞으로 공부해야 할 것입니다! 위에서 말하는 시간복잡도를 무척 큰 폭으로 줄이는데 도움을 주는 애이기도 해요!
우리가 어디서 들어본 스택, 큐, DFS, BFS 모두 알고리즘의 일종이에요. 큐에 대해서 시간복잡도 측면으로 한번 접근해볼까요!?
class Queue {
constructor() {
this.queue = [];
}
enqueue(item) { this.queue.push(item); } // O(1)
dequeue() { return this.queue.shift(); } // O(N)
peek() { return this.queue[0]; } // O(1)
size() { return this.queue.length; } // O(1)
}
const q = new Queue();
q.enqueue(1);
q.enqueue(2);
console.log(q.dequeue()); // 1
console.log(q.peek()); // 2값 넣을때는 뒤로! 뺄때는 앞으로! 빼는 식으로 해서 사실상 넣고 뺄때마다 O(1)이 되는게 맞긴 한데요?
js에서 shift를 하면 결국 모든 값을 앞으로 옮기는 작업이 필요해서 O(N)이 듭니다.
힝 근데 저는 큐도 쓰고싶고 시간복잡도도 챙기구 싶은데용...
링크드리스트라는 알고리즘을 사용해서 만들수는 있답니다.
얘는 배열을 사용하는 방식이 아니고 주솟값을 활용하는 방식이라서 시간복잡도는 아주 좋아요. 물론... 위와같은 방식으로 BFS풀어도 대부분은 문제가 없을거에요! 아래는 링크드 리스트 방식입니다.
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
class Queue {
constructor() {
this.front = this.rear = null;
this.length = 0;
}
enqueue(value) {
const newNode = new Node(value);
if (!this.rear) {
this.front = this.rear = newNode;
} else {
this.rear.next = newNode;
this.rear = newNode;
}
this.length++;
}
dequeue() {
if (!this.front) return null;
const value = this.front.value;
this.front = this.front.next;
if (!this.front) this.rear = null;
this.length--;
return value;
}
peek() { return this.front ? this.front.value : null; }
size() { return this.length; }
}
const q = new Queue();
q.enqueue(1);
q.enqueue(2);
console.log(q.dequeue()); // 1
console.log(q.peek()); // 2
알고리즘은 공식이니까 넘 무서워하지 말기!
하 이거 어케 개발하지..
> 오케이 나 이 알고리즘 쓸거고? 막막하긴 한데? 일단 공식대로 써보자. 로 변하게 해주는 친구다!
